Различают три вида равновесия тел:

- устойчивое;

- неустойчивое;

- безразличное. 

Равновесие называется устойчивым, если после небольших внешних воздействий тело самопроизвольно возвращается в исходное состояние равновесия.

Рассмотрим более подробно устойчивое равновесие для тел не имеющих оси вращения и тел с закрепленной осью вращения.

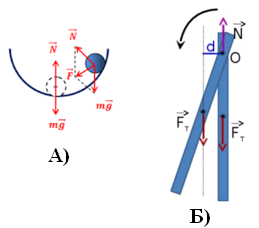
Рис. 53.1. Устойчивое равновесие тел: А) не имеющих оси вращения, Б) с закрепленной осью вращения

На тело, не имеющее оси вращения (рис. 53.1 А),  действуют две силы: сила тяжести и сила реакции опоры. В положении равновесия эти силы компенсируют друг друга и их равнодействующая равна нулю. При отклонении тела от положения равновесия, действующие на него силы уже не будут компенсировать друг друга, так как будут направлены под некоторым углом относительно друг друга, а следовательно их равнодействующая уже не будет равна нулю. Путем построения, легко убедиться, что для любой точки вогнутой поверхности, не совпадающей с положением равновесия, равнодействующая сил тяжести и реакции опоры будет направлена к положению равновесия. Модуль (численное значение) равнодействующей будет пропорционален отклонению от положения равновесия. Основываясь на этом можно утверждать, что признаком устойчивого равновесия будем считать - возникновение силы стремящейся вернуть тело в положение равновесия.

На тело, имеющее закрепленную ось вращения (рис. 53.1 Б), так же действуют две силы: сила тяжести и сила реакции опоры, но как мы помним, для равновесия такого тела необходимо выполнение второго условия равновесия, т.е. правила моментов. Каждая сила, действующая на тело создает свой момент силы, который можно рассчитать по формуле:

M=F∙d.

Анализируя рисунок понимаем, что момент силы реакции опоры N будет равен нулю, так как линия действия силы проходит через ось вращения О и следовательно плечо силы равно нулю. таким образом остается один момент - момент силы тяжести. Из рисунка нетрудно понять, что момент силы тяжести будет стремится вернуть тело в положение равновесия. Таким образом можно сделать вывод, что для тел с закрепленной осью вращения признаком устойчивого равновесия будет являться возникновение момента силы стремящегося вернуть тело в положение равновесия.

Более тщательное рассмотрение рисунка позволяет сформулировать другой признак устойчивого равновесия для тел с закрепленной осью вращения. Обратим внимание на то, что центр масс тела, к которому приложена сила тяжести, при  расположен ниже оси вращения на одной вертикали с ней.

Расположение центра масс ниже оси вращения и будет признаком устойчивого равновесия для тел с закрепленной осью вращения.

Равновесие называется неустойчивым, если при небольшом смещении тела из положения равновесия, тело самопроизвольно не возвращается в исходное положение равновесия.

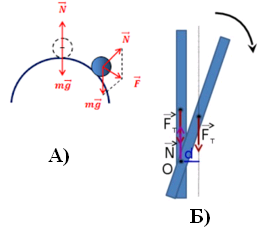
Рис. 53.2. Неустойчивое равновесие тел: А) не имеющих оси вращения, Б) с закрепленной осью вращения

Рассматривая рисунки 53.2 А) и Б), по аналогии с устойчивым равновесием можно сделать вывод о том, что тело не имеющее оси вращения находится в равновесии и равнодействующая приложенных к нему сил отлична от нуля и направлена от положения равновесия. Таким образом признаком неустойчивого равновесия будем считать - возникновение силы стремящейся удалить тело от положения равновесия. В случае с шаром, находящимся на выпуклой поверхности такой силой является равнодействующая сил тяжести и реакции опоры.

Анализируя рисунок, видим, что в положении неустойчивого равновесия центр масс расположен выше оси вращения на одной вертикали с осью вращения, тогда по аналогии с устойчивым равновесием можно сделать вывод. Расположение центра масс выше оси вращения является признаком неустойчивого равновесия для тел с закрепленной осью вращения.

Равновесие называется безразличным, если при небольшом смещении тела из положения равновесия оно самопроизвольно переходит в другое положение равновесия.

Рис. 53.3. Безразличное равновесие тел: А) не имеющих оси вращения, Б) с закрепленной осью вращения

Для тел не имеющих оси вращения признаком безразличного равновесия будет являться равенство нулю равнодействующей приложенных к нему сил при отклонении от исходного положения равновесия.

Для тел с закрепленной осью вращения признаком безразличного равновесия будет совпадения центра масс и оси вращения тела. Действительно, в этом случае все силы оказываются приложенными к одной точке (оси вращения) и линии действия сил проходят через эту точку, тогда плечи сил окажутся равными нулю и при любых отклонениях от положения равновесия моменты возникать не будут.

Содержание