Так как рычаг представляет собой твердое тело с закрепленной осью вращения, то применим второе условие равновесия (правило моментов).

М₁+М₂ – М₃ – М₄ – М₅ = 0

где, для случая представленного на рисунке а)

М₁ = 2mg3d

М₂ = mg2d

М₃ = 2mgd

М₄ = mg2d

М₅ = mg3d

Подставив полученные уравнения в выражение (1), получим:

2mg3d + mg2d - 2mgd - mg2d – mg3d = 0

2mg3d + mg2d = 2mgd + mg2d + mg3d

Вынесем mgd за скобки, получим:

mgd(6 + 2) = mgd(2 + 2 +3)

Получим:

8 = 7

Что является ложным высказыванием, значит рычаг а) не находится в равновесии.

Аналогично решаем для случая б), в результате получаем:

8 = 6

Что также является ложным высказыванием, значит рычаг б), также не находится в равновесии.

Центр масс системы обладает свойством, говорящем о том, что, если ось вращения системы проходит через центр масс, то система находится в равновесии.

Пусть т. О является центром масс системы двух шаров и стержня, тогда условие равновесия для этой системы примет вид:

 или ,

где:

 - момент силы тяжести, приложенной к шару массой

- момент силы тяжести, приложенной к шару массой m₂

 - момент силы тяжести, приложенной к стержню.

Плечи каждой из сил, определим с помощью рисунка и выразим их через плечо d₂:

.

Подставим полученные выражения в выражения для моментов сил, а затем в правило моментов:

.

Преобразовав данное уравнение получим:

Выразим из этого равенства d₂:

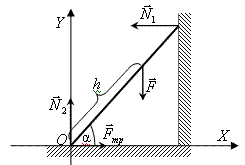
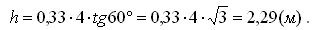На лестницу действуют силы:

- F - сила давления со стороны человека ;

- N₁ - сила реакции стены ;

- N₂ - сила реакции пола;

- F_тр - сила трения между полом и лестницей.

Сделаем рисунок, на котором покажем: лестницу, действующие на нее силы и координатные оси ОХ и ОУ.

Запишем первое условие равновесия для лестницы:

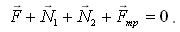
В проекциях на выбранные оси уравнение примет вид:

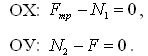
В случае скольжения лестницы, ось вращения начнет перемещаться вдоль пола, поэтому необходимо записать второе условие равновесия, т.е. правило моментов.

М₁=М₂.

где М₁ – момент силы давления со стороны человека, М₂ – момент силы реакции стены, моменты силы трения и силы реакции пола равны нулю, так как линии действия этих сил проходят через ось вращения.

Раскроем выражения для моментов полученных сил:

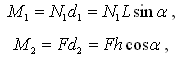
тогда:

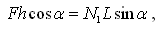
отсюда:

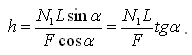
Решая систему уравнений:

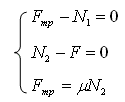
приходим к выводу, что:

тогда:

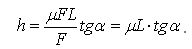
Подставляя численные значения, получим: