|
В соответствии с вторым законом Ньютона
ускорение тела прямопропорционально приложенной силе.
Легко доказать, что угловое ускорение
прямопропорционально моменту силы действующей на
вращающееся тело, для этого достаточно рассмотреть
движение точки по окружности радиусом -
R.
Запишем второй закон Ньютона для
рассматриваемой точки:
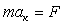
Умножив обе части уравнения на радиус
окружности (R),
описываемой точкой
получим:
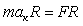 . .
Учитывая выражение для момента силы и
выражение связывающее угловое ускорение с касательным
получим:
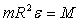 . .
Произведение массы материальной точки
на квадрат расстояния до оси вращения называется
моментом инерции материальной точки. Момент инерции
обозначают I.

С учетом понятия момента инерции
предыдущее равенство можно записать в виде:
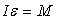 . .
Данное уравнение называют основным
уравнение динамики вращательного движения. Это уравнение
справедливо и для вращательного движения твердого тела,
имеющего неподвижную ось вращения, где
I - момент
инерции твердого тела, а М - суммарный момент
силы действующий на тело.
Любое тело можно представить как
совокупность материальных точек - разноудаленных от оси
вращения, тогда момент инерции тела будет равен сумме
моментов инерции отдельных точек:
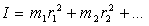
Таким образом можно утверждать, что
момент инерции характеризует распределение массы
относительно оси вращения.
Приведем выражения для моментов инерции
для некоторых абсолютно твердых однородных тел массой
m.
Тонкий прямой стержень длиной
l:
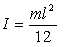 . .
Прямой цилиндр или диск, относительно
оси совпадающей с геометрической осью:
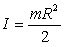 . .
Шар, относительно оси проходящей через
центр:
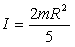 . .
Тонкий обруч, относительно оси
проходящей через центр:
 . .
Рассмотрим вращающийся диск, импульс
каждой отдельной точки диска отличен от нуля, причем чем
дальше от центра диска расположена точка, тем большим
импульсом она обладает, так как линейная скорость
пропорциональна радиусу окружности описываемой точкой, а
угловая скорость у всех точек твердого тела равна нулю.
Суммарный же импульс всего тела равен нулю, так как
каждой точке можно поставить в соответствие симметричную
ей относительно оси вращения точку, движущуюся в
противоположную сторону.
Следовательно, необходимо ввести еще
одну величину, характеризующую движение точек,
составляющих твердое тело, по окружности в зависимости
от удаленности этих точек от оси вращения. Такая
величина называется моментом импульса. |
