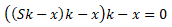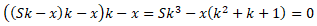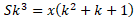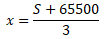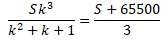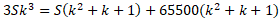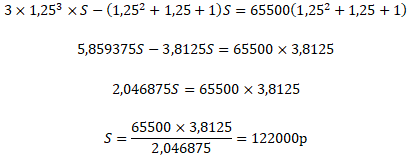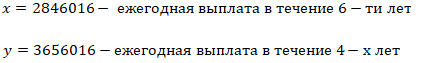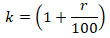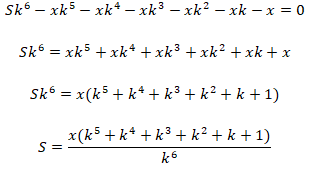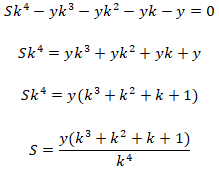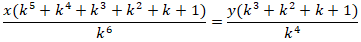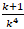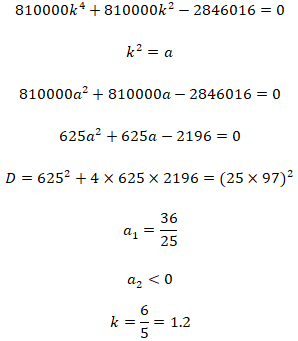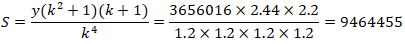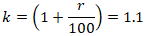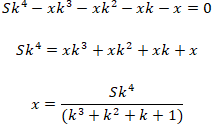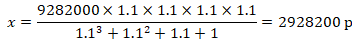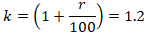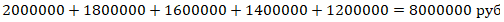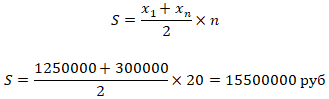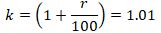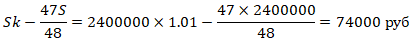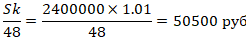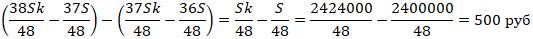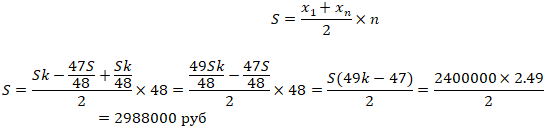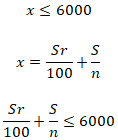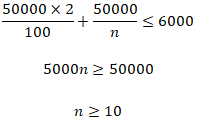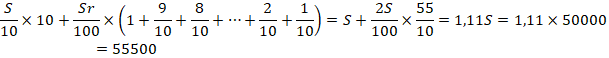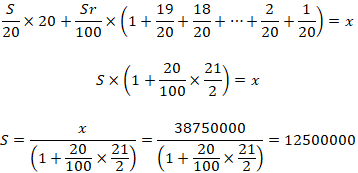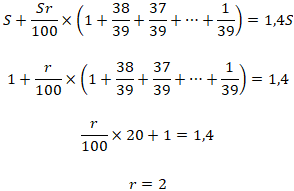|
Задачи на выплаты с постоянными платежами: |
|
№1. Сергей Сергеевич хочет взять в кредит 2 млн рублей с процентной ставкой 20%: годовых. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов.
Сделайте расчет кредита, если Сергей Сергеевич ежегодно планирует вносить 600 тыс. рублей. Какую сумму Сергей Сергеевич выплатит банку за весь период кредитования?
|
Решение:
Посмотрим, что нам известно:
S = 2000000 рублей – начальный
долг
r = 20% годовых – процентная
ставка
x= 600000 рублей – ежегодный
платеж
Экономические задачи легче всего
решать, составляя таблицу, поэтому так и сделаем.
Данную задачу проще всего решать
простым заполнением таблицы, поэтому высчитываем
недостающие данные и записываем их в таблицу.
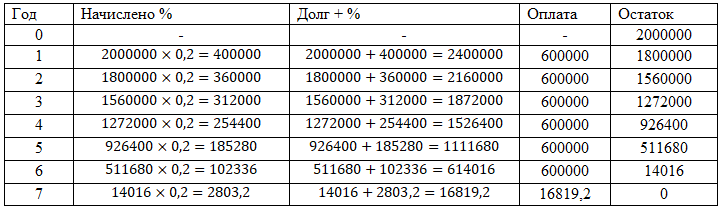
Год, когда Сергей Сергеевич взял кредит, обозначим
нулевым, в этот год мы не погашаем кредит. Далее, в
начале года, на остаток начисляется процент банка, и
только после этого мы вносим свои 600 тыс., теперь наш
остаток составляет 1,8 млн. и т.д.
Ответом на эту задачу будет вся сумма, которую Сергей
Сергеевич выплатит банку за весь период кредитования,
поэтому мы просто складываем все значения со столбика
«оплата»:
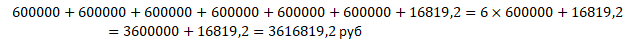
|
|
Ответ: 3616819,2 руб |
|
------------------------------------------------------------ |
|
№2.
31 января 2018 года Петр Петрович взял в банке 6327000 рублей в кредит
под 12% годовых. Схема выплаты кредита следующая: 1
января каждого следующего года банк начисляет проценты
на оставшуюся часть долга (то есть увеличивает долг на
12%), затем в течение календарного года Петр Петрович
переводит в банк ежегодный платеж. Какой должна быть
сумма ежегодного платежа, чтобы Петр Петрович выплатил
долг тремя равными платежами (то есть за три года)?
|
Решение:
Запишем что нам известно:
S = 6 327 000 руб. – сумма
долга
r = 12% – процентная ставка
3 года
Обозначим величину, на которую
повышается долг за k:
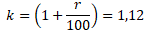
Составим таблицу:

Ответом на задачу является сумма
ежегодного платежа, чтобы ее найти воспользуемся
уравнением из таблицы:
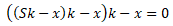
Преобразуем уравнение
(раскроем скобки):
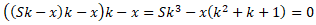
Перенесем часть уравнения в правую
часть:
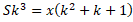
Выразим x:
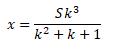
Подставим значения:
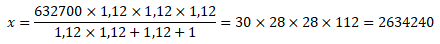
|
|
Ответ:
2634240 руб |
|
------------------------------------------------------------ |
№3. В июле 2015 года
Николай Николаевич взял кредит в банке на некоторую
сумму. Условия его возврата были таковы:
- каждый январь долг возрастал на 25% по сравнению с
концом предыдущего года;
- с февраля по июнь каждого года Николай Николаевич
выплачивал некоторую часть долга.
Определите, на какую сумму был взят кредит, если
известно, что кредит был выплачен тремя равными
платежами (т.е. за три года) и общая сумма выплат
оказалась на 65500 рублей больше суммы взятого кредита.
|
Решение:
Выпишем что нам известно:
r = 25% – процентная ставка
x – 1 выплата
S – долг до начисления
процентов
3 года
Обозначим величину, на которую повышается долг за
k:
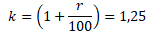
Также нам известно, что 3 выплаты на 65500 больше, чем
сумма, взятая в кредит:
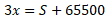 (1)
(1)
Составим таблицу:

Для решения задачи воспользуемся
уравнением:
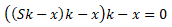
Преобразуем уравнение
(раскроем скобки):
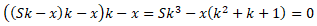
Перенесем часть уравнения в правую
часть:
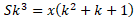
Выразим x:

Теперь выразим X
в уравнении (1):
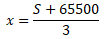
Приравняем правые части двух
уравнений:
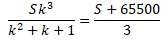
Воспользуемся правилом пропорции:
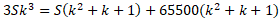
Преобразуем уравнение и подставим
значения:
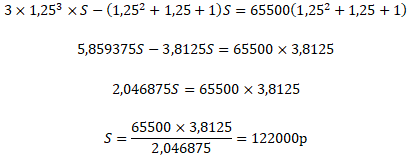
|
|
Ответ:
122000 р |
|
------------------------------------------------------------ |
№4.
В марте 2014 года Петр
Петрович взял в банке некоторую сумму в кредит под
некоторый процент годовых. Схема выплаты кредита
следующая: 1 января каждого следующего года банк
начисляет проценты на оставшуюся часть долга (то есть
увеличивает долг на
r%),
затем в течение месяца Петр Петрович переводит в банк
очередной платеж. Если он будет платить каждый год по 2
846 016 рублей, то выплатит долг за 6 лет. Если по
3 656 016 рублей, то за 4 года. Какую сумму взял в
кредит Петр Петрович и под какой процент годовых?
|
Решение:
Выпишем что нам известно:
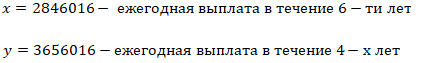
S
– долг до начисления процентов
r%
– процентная ставка
Обозначим величину, на которую повышается долг за
k:
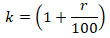
Составим две таблицы погашения долга за 6 и за 4 года.

Выпишем уравнение первой таблицы
и преобразуем его в уравнение (1):
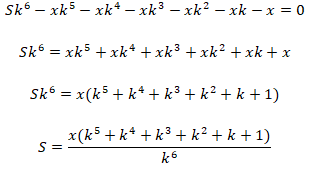
Выпишем уравнение второй таблицы
и преобразуем его в уравнение (2):
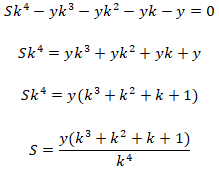
Так как сумма, внесенная в банк, в первом и во втором
случае одинакова, то мы можем приравнять правые части
обоих уравнений:
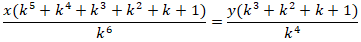
Вынесем (k+1)
за скобку и сократим обе стороны на
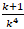 : :
Подставим значения и избавимся от минуса:
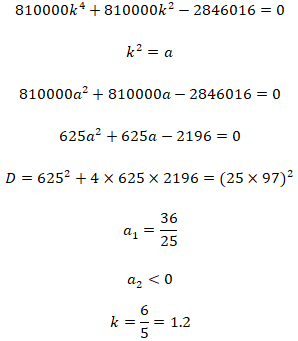
Следовательно
r=20%
2) Найдем изначальный вклад:
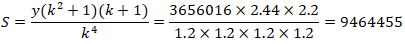
|
|
Ответ:
20% и 9464455р |
|
------------------------------------------------------------ |
№5.
25 января 2018 года Николай Николаевич взял в банке
9282000 рублей в кредит под 10% годовых. Схема выплаты
кредита следующая: 1 января каждого следующего года банк
начисляет проценты на оставшуюся часть долга (то есть
увеличивает долг на 10%), затем в течение календарного
года Николай Николаевич переводит в банк ежегодный
платеж. Какой должна быть сумма ежегодного платежа,
чтобы Николай Николаевич выплатил долг четырьмя равными
платежами (то есть за четыре года)?
|
Решение:
Выпишем что нам известно:
r=10%
годовых
S=9282000
рублей – сумма взятая в кредит
n=4
года
Обозначим величину, на которую повышается долг за
k:
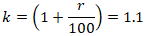
Составим таблицу:

Выпишем получившееся уравнение:
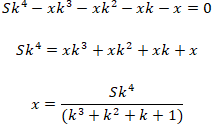
Подставим значения и сократим:
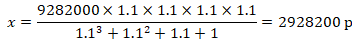
|
|
Ответ:
2928200 р |
|
------------------------------------------------------------ |
|
|
|
Схема выплат кредита с равномерным погашением основного
долга: |
№1.
В июле планируется взять кредит в банке на сумму 5 000
000 рублей на 5 лет. Условия его возврата таковы:
—каждый январь долг возрастает на 20% по сравнению с
концом предыдущего года:
— с февраля по июнь каждого года необходимо выплатить
часть долга;
— в июле каждого года долг должен быть на одну и ту же
величину меньше долга на июль предыдущего года.
а) Сколько рублей составила общая сумма выплат после
погашения кредита?
б) Какова будет сумма выплат, если на этих же условиях
взять кредит на 20 лет?
|
Решение:
Дано:
S=5000000
р
n=5
лет
r=20%
Обозначим величину, на которую повышается долг за
k:
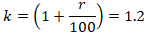
Составим таблицу:
Так как долг должен быть на одну и ту же величину меньше
предыдущего долга, то разделим столбики на «долг
+ %» и
«оплата»
Узнаем сумму дога в конце каждого года, так как он
меньше на одну и ту же величину долга предыдущего года,
то просто разделим сумму на количество лет
5000000:5=1000000
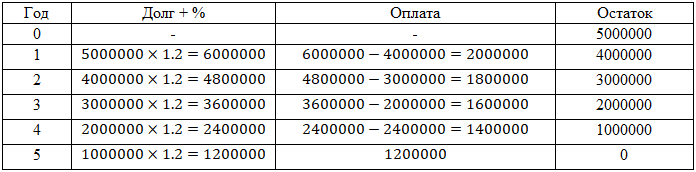
А) Все выплаты:
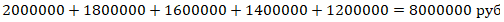
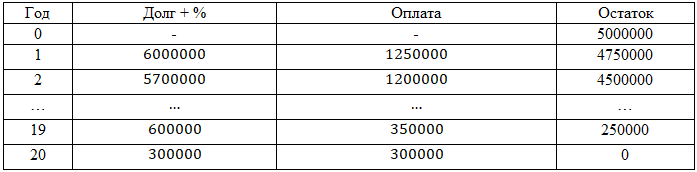
б) Узнаем сумму выплат за 20 лет,
составим такую же таблицу и посчитаем, на сколько
уменьшается долг каждый год 5000000:20=250000
По формуле суммы арифметической
прогрессии вычисляем сумму выплат за 20 лет
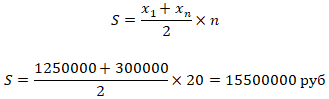
|
|
Ответ:
8000000;
15500000 |
|
------------------------------------------------------------ |
№2.
15-го января планируется взять кредит в банке на сумму
2,4 млн рублей на 48 месяцев. Условия его возврата
таковы:
— 1-го числа каждого месяца долг возрастает на 1% по
сравнению с концом предыдущего месяца:
— со 2-го по 14-е число месяца необходимо выплатить
часть долга;
— 15-го числа каждого месяца долг должен быть на одну и
ту же величину меньше долга на 15-е число предыдущего
месяца.
а) Сколько рублей составит первый платеж?
б) Сколько рублей составит последний платеж?
в) На сколько рублей 11-й платеж превосходит 12-й?
г) Какую сумму в рублях нужно вернуть банку за весь
срок кредитования? |
Решение:
Дано:
S=2400000
руб
n=48
мес.
r=1%
Обозначим величину, на которую повышается долг за
k:
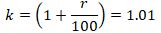
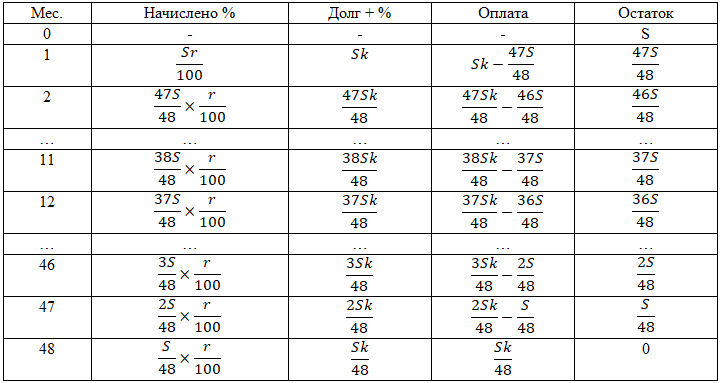
Составим таблицу, для упрощения
сократим ее и выпишем только нужные для решения
промежутки времени
а) Сколько рублей составит
первый платеж, смотрим таблицу, выписываем нужное нам
выражение, подставляем значения и считаем:
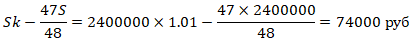
б) Сколько рублей составит
последний платеж?
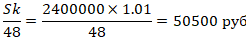
в) На сколько рублей 11-й платеж превосходит 12-й?
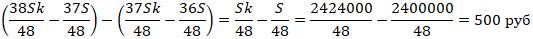
г) Какую сумму в рублях нужно вернуть банку за весь
период кредитования?
Воспользуемся формулой суммы арифметической прогрессии
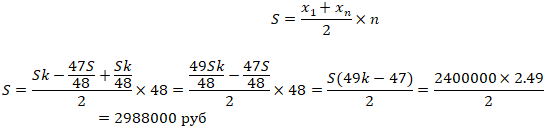
|
|
Ответ:
74000; 50500; 500; 2988000 |
|
------------------------------------------------------------ |
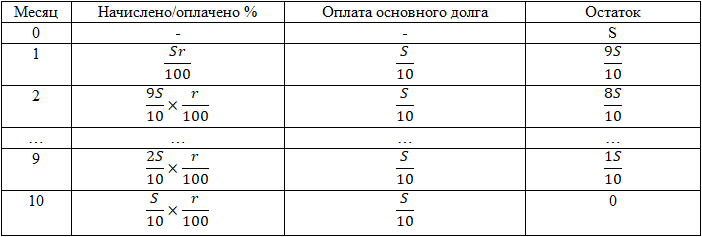
№3.
15-го августа планируется взять кредит в банке для
покупки
Apple iPhone X
в размере 50000 рублей.
Условия возврата таковы:
— 1 числа каждого месяца долг возрастает на 2% по
сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо
выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и
ту же сумму меньше долга на 15-е число предыдущего
месяца.
А) На какой минимальный срок следует брать кредит, чтобы
наибольший месячный кредит не превысил 6000 рублей?
Б) Какова при этом будет сумма всех выплат банку после
погашения кредита?
|
Решение:
Дано:
S=50000
руб
r=2%
x≤6000
руб
А) Пусть
n
мес. срок кредита, т.к. наибольший платеж это первый, то
получаем:
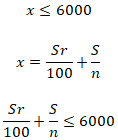
Подставляем значения:
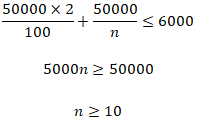
Следовательно, минимальный срок при таких условиях равен
10 месяцам.
Б) С учетом предыдущего пункта составляем таблицу на 10
месяцев:
Теперь считаем сумму всех выплат,
она будет равна сумме всех оплаченных процентов и
основного долга:
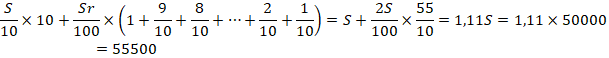
|
|
Ответ:
10 мес; 55500 руб |
|
------------------------------------------------------------ |
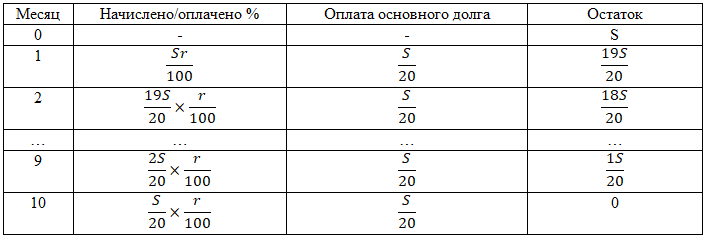
№4.
В июле планируется взять в банке ипотечный кредит на
срок 20 лет под 20% годовых.
Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с
концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить
часть долга;
— в июле каждого года долг должен быть на одну и ту же
величину меньше долга на июль предыдущего года.
Найти сумму, взятую в кредит, если известно, что общая
сумма выплат после его погашения составит 38 млн. 750
тыс. рублей.
|
Решение:
Дано:
n=20
лет
r=
20%
x=38750000
руб
Составим таблицу:
Составим уравнение, все выплаты
равняются сумме долга и всех оплаченных процентов:
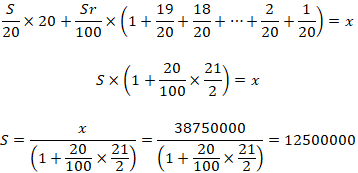
|
|
Ответ:
12500000 рублей |
|
------------------------------------------------------------ |
№5.
15-го января планируется взять кредит в банке на 39
месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на
r%
по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число месяца необходимо выплатить
часть долга
— 15-го числа каждого месяца долг должен быть на одну и
ту же величину меньше долга на 15-е число предыдущего
месяца.
Известно, что общая сумма выплат после полного погашения
кредита на 40% больше суммы, взятой в кредит. Найдите
процентную ставку банка
r.
|
Решение:
Дано:
n=39
мес
x=
1,4S
Составим таблицу:
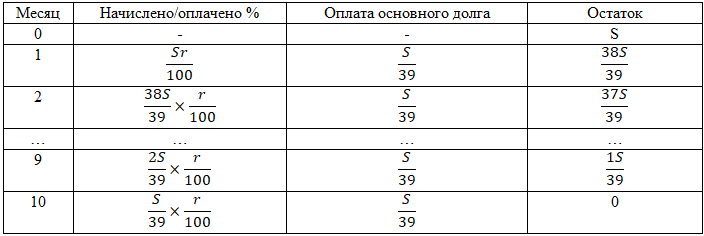
По условию:
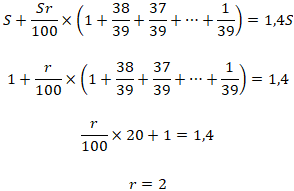
|
|
Ответ:
2% |
|
------------------------------------------------------------ |
|
Содержание |
| |
|
|


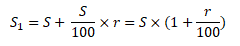
 заменяют
на букву
заменяют
на букву 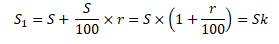
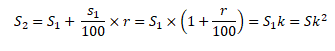
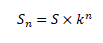
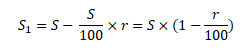
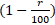 мы
также можем заменить на
мы
также можем заменить на 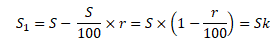

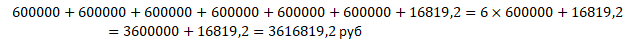
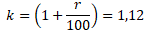

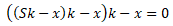
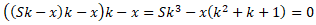
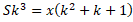
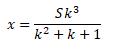
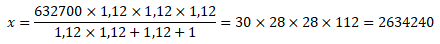
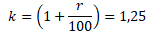
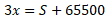 (1)
(1)