|
|
| Добро пожаловать в
пользовательский раздел сайта! |
| |
| Библиотека
: Физика : Задачи для самостоятельного
решения. Тема 12 -
Электромагнитные колебания и волны. |
|
|
|
|
|
Свободные электромагнитные колебания.
Колебательный контур. |
|
№12.1
Как изменится частота собственных
электромагнитных колебаний в контуре (см.
рисунок), если ключ К перевести из положения 1 в
положение 2?
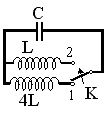
Ответ: Увеличится в 2 раза.
№12.2
Найти период и частоту колебаний в контуре, состоящем из
конденсатора емкостью С = 800 пФ и катушки
индуктивностью L = 2 мкГн. Во сколько раз изменится
период колебаний, если в конденсатор ввести диэлектрик
с диэлектрической проницаемостью ε = 9?
Ответ: 250
нс; 4 МГц; увеличится в 3 раза.
№12.3
Каков диапазон частот собственных колебаний в контуре,
если его индуктивность можно изменять в пределах от 0,1
до 10 мкГн, а емкость — в пределах от 50 до 5000 пФ?
Ответ: От
710 кГц до 71 МГц.
№12.4
Катушку какой индуктивности надо включить в
колебательный контур, чтобы при емкости конденсатора 50
пФ получить частоту свободных колебаний 10 МГц?
Ответ: 5,1
мкГн.
№12.5
Во сколько раз изменится частота собственных колебаний в
колебательном контуре, если емкость конденсатора
увеличить в 25 раз, а индуктивность катушки уменьшить в
16 раз?
Ответ:
Уменьшится в 1,25 раза.
№12.6
При увеличении емкости конденсатора колебательного
контура на 0,08 мкФ частота колебаний уменьшилась в 3
раза. Найти первоначальную емкость конденсатора.
Индуктивность катушки осталась прежней.
Ответ:
0,01 мкФ.
№12.7
В наборе радиодеталей для изготовления простого
колебательного контура имеются две катушки с
индуктивностями L1 = 1 мкГн
и L2 = 2 мкГн,
а также два конденсатора, емкости которых C1 = 3 пФ
и C2 = 4 пФ.
При каком выборе двух элементов из этого набора частота
собственных колебаний контура будет наибольшей?
Ответ: L1 и
C1.
№12.8
Колебательный контур состоит из конденсатора емкостью
400 пФ и катушки индуктивностью 10 мГн. Найти амплитуду
колебаний силы тока, если амплитуда колебаний напряжения
500 В?
Ответ: 0,1
А.
№12.9
В колебательном контуре индуктивность катушки 0,2 Гн, а
амплитуда колебаний силы тока 40 мА. Найти энергию
электрического поля конденсатора и магнитного поля
катушки в тот момент, когда мгновенное значение силы
тока в 2 раза меньше амплитудного значения.
Ответ: 120
мкДж; 40 мкДж.
№12.10
Амплитуда силы тока в контуре 1,4 мА, а амплитуда
напряжения 280 В. Найти силу тока и напряжение в тот
момент времени, когда энергия магнитного поля катушки
равна энергии электрического поля конденсатора.
Ответ: 1
мА; 200 В.
№12.11
Катушка с индуктивностью 31 мГн присоединена к плоскому
конденсатору с площадью каждой пластины 20 см2
и расстоянием между ними 1 см. Чему равна
диэлектрическая проницаемость среды, заполняющей
пространство между пластинами, если амплитуда колебаний
силы тока в контуре 0,2 мА и амплитуда напряжения 10 В?
Ответ: 7.
№12.12
Емкость конденсатора колебательного контура 1 мкФ,
индуктивность катушки 0,04 Гн, а амплитуда колебаний
напряжения 100 В. В данный момент времени напряжение на
конденсаторе равно 80 В. Найти:
1)
Амплитуду колебаний силы тока;
2)
Полную энергию;
3)
Энергию электрического поля;
4)
Энергию магнитного поля;
5)
Значение силы тока в данный момент.
Ответ: 0,5
А; 5∙10-3
Дж; 3,2∙10-3
Дж; 1,8∙10-3
Дж; 0,3 А.
№12.13
Амплитуда колебаний напряжения в контуре 100 В, частота
колебаний 5 МГц. Через какое время напряжение впервые
будет равно 71 В?
Ответ: 25
нс.
№12.14
В таблице показано, как изменялся заряд конденсатора в
колебательном контуре с течением времени.
|
t,
10–6 c |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
q,
10–9
Кл |
2 |
1,42 |
0 |
–1,42 |
–2 |
–1,42 |
0 |
1,42 |
2 |
1,42 |
Вычислите по
этим данным максимальное значение силы тока в катушке.
Ответ: 1,6
мА.
№12.15
В момент времени
t
заряд конденсатора в идеальном колебательном контуре
равен 4∙10-9 Кл, а сила тока в катушке равна
3 мА. Амплитуда заряда
qm
=
5∙10-9 Кл. Найдите период колебаний в
контуре.
Ответ: 6,28 мкс.
№12.16
В идеальном колебательном контуре амплитуда колебаний
силы тока
Iт
=
5 мА, а амплитуда напряжения на конденсаторе
Um
=
2,0 В. В некоторый момент времени напряжение на
конденсаторе равно 1,2 В. Найдите силу тока в контуре в
этот момент.
Ответ: 4
мА.
№12.17
Написать уравнения зависимости напряжения и силы тока от
времени для электроплитки сопротивлением 50 Ом,
включенной в сеть переменного тока с частотой 50 Гц и
напряжением 220 В.
Ответ:
u = 310cos100πt; i = 6,2cos100πt.
№12.18
По
графику найти амплитудное значение переменной
ЭДС, ее период и частоту. Записать формулу
изменения ЭДС со временем.
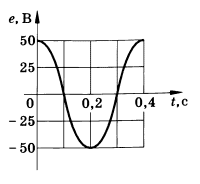
Ответ: 50 В; 0,4 с; 2,5 Гц; е = 50
cos5πt.
№12.19
Заряд на пластинах конденсатора колебательного контура
изменяется с течением времени в соответствии с
уравнением q=10-6cos(104π∙t).
Записать уравнение зависимости силы тока от времени.
Найти период и частоту колебаний в контуре, амплитуду
колебаний заряда и амплитуду колебаний силы тока.
Ответ:
i=-0,01π sin(104π∙t) ;
0,2 мс; 5 кГц; 1 мкКл; 31,4 мА.
№12.20
Колебательный контур состоит из конденсатора емкостью 1
мкФ и катушки индуктивностью 4 Гн. Амплитуда колебаний
заряда на конденсаторе 100 мкКл. Написать уравнения
зависимости от времени заряда, силы тока и напряжения.
Найти амплитуду колебаний силы тока и напряжения.
Ответ:
q=10-4cos(500∙t) ;
i=-0,05sin(500∙t) ;
u=100cos(500∙t) ;
50 мА; 100 В.
№12.21
Емкость конденсатора колебательного контура 0,4 мкФ,
частота собственных колебаний 50 кГц, амплитуда
колебаний заряда 8мкКл. Написать уравнения зависимости
от времени заряда, силы тока и напряжения. Найти
амплитуду колебаний напряжения, силы тока и
индуктивность катушки.
Ответ:
q=8∙10-8cos(105π∙t) ;
u=20cos(105π∙t);
i=-2,5sin(105π∙t);
20 В; 2,5 А; 25 мкГн.
№12.22
№12.23
№12.24
№12.25
|
|
Переменный электрический ток.
Трансформаторы. |
|
№12.26
Трансформатор, содержащий в первичной обмотке 840
витков, повышает напряжение с 220 до 660 В. Каков
коэффициент трансформации? Сколько витков содержится во
вторичной обмотке? В какой обмотке провод имеет большую
площадь поперечного сечения?
Ответ:
1/3; 2520; в первичной.
№12.27
Чтобы узнать сколько витков содержится в первичной и
вторичной обмотках трансформатора, на вторичную катушку
намотали 11 витков провода. При включении первичной
обмотки в сеть с напряжением 220 В вольтметр показал,
что на обмотке с 11 витками напряжение равно 4,4 В, а на
вторичной обмотке – 12 В. Сколько витков в первичной и
вторичной обмотках?
Ответ:
550; 30.
№12.28
Понижающий трансформатор с коэффициентом трансформации,
равным 10, включен в сеть с напряжением 220 В. Каково
напряжение на выходе трансформатора, если сопротивление
вторичной обмотки 0,2 Ом, а сопротивление полезной
нагрузки 2 Ом?
Ответ: 20
В.
№12.29
Трансформатор включен в сеть с переменным напряжением
220 В. Напряжение на зажимах вторичной обмотки равно 20
В, ее сопротивление 1 Ом, сила тока во вторичной обмотке
2 А. Найти коэффициент трансформации и КПД
трансформатора пренебрегая потерями в первичной обмотке
и сердечнике.
Ответ: 10;
90,9%.
№12.30
Сила тока в первичной обмотке трансформатора 0,5 А,
напряжение на ее концах 220 В. Сила тока во вторичной
обмотке 11 А, напряжение на ее концах 9,5 В. Определить
КПД трансформатора.
Ответ: КПД
трансформатора равен 95%.
№12.31
Сколько витков имеет рамка площадью 500 см2,
если при вращении ее с частотой 20 Гц в однородном
магнитном поле индукцией 0,1 Тл амплитудное значение ЭДС
равно 63 В?
Ответ: 100.
№12.32
Какое значение принимает напряжение через 10, 15 и 30
мс, если амплитуда напряжения 200 В и период 60 мс?
Ответ: 100
В; 0 В; - 200 В.
№12.33
Найти амплитуду ЭДС, наводимой при вращении
прямоугольной рамки в горизонтальном магнитном поле
частотой 50 Гц, если площадь рамки 100 см2,
а индукция магнитного поля 0,2 Тл. Начальная фаза равна
нулю.
Ответ:
Амплитуда ЭДС, возникающей в рамке будет равна 628 мВ.
№12.34
На какое напряжение надо рассчитывать изоляторы линии
передачи, если действующее напряжение 430 кВ?
Ответ: 610
кВ.
№12.35
Ток в цепи меняется по гармоническому
синусоидальному закону. Мгновенное
значение силы тока для фазы π/6 равно 6 А. Определить
амплитудное и действующее значения силы тока.
Ответ: 12
А; 8,5 А.
Резонанс
в колебательном контуре.
№12.36
В цепь включены конденсатор емкостью 2 мкФ и катушка
индуктивностью 0,005 Гн. При какой частоте тока в этой
цепи будет резонанс?
Ответ: 10
кГц.
№12.37В цепь переменного тока с частотой 400 Гц включена
катушка индуктивностью 0,1 Гн.
Конденсатор какой емкости надо включить в эту цепь,
для возникновения резонанса?
Ответ: 1,6
мкФ.
№12.38
В таблице показано, как изменялся заряд конденсатора в
колебательном контуре, подключенном к источнику
переменного тока. При какой индуктивности катушки в
контуре наступит резонанс, если емкость конденсатора
равна 50 пФ?
|
T, 10–6 c |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
q , 10–9
Кл |
2 |
1,42 |
0 |
–1,42 |
–2 |
–1,42 |
0 |
1,42 |
2 |
1,42 |
Ответ: Чтобы в контуре возник резонанс, индуктивность
катушки должна быть равна 32 мГн.
№12.39
№12.40
|
|
Электромагнитные волны. |
|
№12.41
Радиостанция ведет передачу и при этом излучает
электромагнитные волны диной 4 метра. На какой частоте
работает радиостанция и к какому частотному диапазону
она принадлежит?
Ответ: 75
МГц; УКВ.
№12.42
Радиостанция «Дорожное радио» вещает в Вязьме на частоте
103,2 МГц (частотный диапазон
FM).
Электромагнитные волны какой длины излучает антенна
радиостанции?
Ответ:
2,9 м.
№12.43
Катушка приемного контура радиоприемника имеет
индуктивность 1 мкГн. Какова емкость конденсатора, если
идет прием станции, работающей на длине волны 1 км?
Ответ:
0,28 мкФ.
№12.44
Радиоприемник настроен на радиостанцию, работающую на
длине волны 25 м. Во сколько раз нужно изменить емкость
колебательного контура радиоприемника, чтобы настроится
на длину волны 31 м?
Ответ:
1,54.
№12.45
При изменении силы тока в катушке индуктивности на 1 А
за 0,6 с в ней индуцируется ЭДС, равная 0,2 мВ. Какую
длину будет иметь радиоволна, излучаемая генератором,
колебательный контур которого состоит из этой катушки и
конденсатора емкостью 14,1 нФ?
Ответ:
2450 м.
|
|
№12.46
В каком диапазоне длин волн работает приемник, если
емкость конденсатора в его колебательном контуре можно
плавно изменять от 200 до 1800 пФ, а индуктивность
катушки постоянна и равна 60 мкГн?
Ответ: 206
– 619 м.
№12.47
Сила тока в открытом колебательном контуре изменяется по
закону: i=0,1cos(6∙105πt) . Найти длину
излучаемой волны.
Ответ:
1000 м. |
|
№12.48
Определить длину электромагнитной волны в вакууме, на
которую настроен колебательный контур, если максимальный
заряд конденсатора 20 нКл, а максимальная сила тока в
контуре 1 А.
Ответ: 38
м.
|
|
№12.49
Сколько колебаний происходит в электромагнитной волне с
длиной волны 300 м за время, равное периоду звуковых
колебаний с частотой 2000 Гц?
Ответ: 500. |
|
№12.50
На каком расстоянии от антенны радиолокатора находится
объект, если отраженный от него радиосигнал возвратился
обратно через 200 мкс?
Ответ: 30
км. |
|
|
|
Задачи повышенной сложности. |
|
№12.51
В таблице показано, как изменялся заряд конденсатора в
колебательном контуре с течением времени. Какова энергия
магнитного поля катушки в момент времени 5·10–6
с, если емкость конденсатора равна 50 пФ?
|
T,
10–6
c |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
q
, 10–9 Кл |
2 |
1,42 |
0 |
–1,42 |
–2 |
–1,42 |
0 |
1,42 |
2 |
1,42 |
Ответ:
Энергия магнитного поля равна 20 нДж.
|
|
№12.52
В идеальном колебательном контуре амплитуда колебаний
силы тока в катушке индуктивности 5 мА, а амплитуда
колебаний заряда конденсатора 2,5 нКл. В момент времени
t сила тока в катушке равна 3 мА. Найдите заряд
конденсатора в этот момент.
Ответ: В
момент времени, когда сила тока в контуре будет равна 3
мА, на обкладках конденсатора заряд будет равен 2 нКл.
|
|
|
|
№12.53
Простой колебательный контур содержит конденсатор
емкостью С = 1 мкФ и катушку индуктивности
L
=
0,01 Гн. Какой должна быть емкость конденсатора, чтобы
циклическая частота колебаний электрической энергии в
контуре увеличилась на ∆ω = 2∙104 с-1?
Ответ: Для увеличения циклической частоты колебаний
электрической энергии в контуре на ∆ω = 2∙104
с-1, в контур нужно включить конденсатор
емкостью 0,25 мкФ.
|
|
------------------------------------------------------------------------ |
|
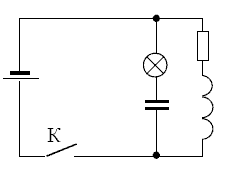
№12.54
В электрической цепи, показанной на рисунке, ЭДС
источника тока равна 12 В, емкость конденсатора
2 мФ, индуктивность катушки 5 мГн, сопротивление
лампы 5 Ом и сопротивление резистора 3 Ом. В
начальный момент времени ключ К замкнут. Какая
энергия выделится в лампе после размыкания
ключа? Внутренним сопротивлением источника тока,
а также сопротивлением катушки и проводов
пренебречь.
|
 |
|
Решение:
Пока ключ
замкнут, через катушку L течет ток I,
определяемый только сопротивлением резистора (так как
внутренним сопротивлением источника пренебрегаем по
условию задачи, а цепи конденсатора при замкнутом ключе
тока нет, то полное сопротивление цепи будет равно
сопротивлению резистора)::
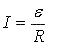
Конденсатор заряжен до
напряжения: U = ε, тогда:
энергия
электромагнитного поля в катушке:
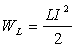 , ,
энергия электромагнитного поля в
конденсаторе:
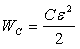 . .
После размыкания ключа, участок
цепи, состоящий из лампы, конденсатора, катушки и резистора будет
представлять собой колебательный контур, в котором начнутся затухающие (так
как контур обладает активным сопротивлением) электромагнитные колебания, и
вся энергия, запасенная в конденсаторе и катушке, выделяется в лампе и на
резисторе:
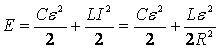 . .
Подсчитаем полную выделившуюся
энергию:
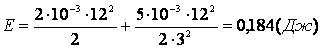 . .
Согласно закону Джоуля–Ленца,
выделяемая на резисторе мощность пропорциональна его сопротивлению.
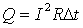 . .
Следовательно, энергия 0,184 Дж
выделяется в лампе и на резисторе пропорционально их сопротивлениям, и на
лампу приходится:
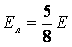 , ,
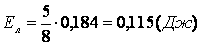 . . |
|
Ответ: На лампе
выделится 0,115 Дж энергии.
------------------------------------------------------------------ |
|
|
|
№12.55
В колебательном контуре конденсатору емкостью 10 мкФ
сообщили заряд 40 мкКл, после чего в контуре возникли
затухающие электромагнитные колебания. Какое количество
теплоты выделится к моменту, когда максимальное
напряжение на конденсаторе станет меньше начального
максимального напряжения в 4 раза?
Ответ: В
колебательном контуре выделится 75 мкДж теплоты.
|
|
№12.56
Конденсатор колебательного контура подключен к источнику
постоянного напряжения (см. рисунок). Графики А и Б
представляют изменения физических величин,
характеризующих колебания в контуре после переведения
переключателя К в положение 2. Установите соответствие
между графиками и физическими величинами, зависимости
которых от времени эти графики могут представлять. К
каждой позиции первого столбца подберите соответствующую
позицию второго и запишите в таблицу выбранные цифры под
соответствующими буквами. |
|
|
|
1)
заряд левой обкладки конденсатора
2)
сила тока в катушке
3)
энергия электрического поля конденсатора
4)
энергия магнитного поля катушки
Ответ: 14.
|
|
|
|
|
|
|
|
№12.57
Разность потенциалов на обкладках конденсатора
колебательного контура меняется по закону
.
Емкость конденсатора 0,9 мкФ. Найти индуктивность
контура, амплитуду силы тока в контуре, а также длину
волны, соответствующую излучению этого контура.
Ответ:
Индуктивность контура равна 1,1 мГн; амплитуда силы тока
в контуре равна 1,43 А; длина волны, соответствующая
излучению контура составляет 60 км.
|
|
------------------------------------------------------------------------- |
|
№12.58
Колебательный контур состоит из катушки
индуктивности и четырех конденсаторов, соединенных, как
показано на рисунке. Во сколько
раз k
изменится период собственных колебаний в контуре, если
замкнуть ключ, соединяющий точки А и В? Емкости
конденсаторов С1=10-8 Ф, С2=
4∙10-8 Ф. |
Решение:
Запишем формулу Томсона, позволяющую
рассчитывать период колебаний в контуре:
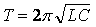
тогда период колебаний до замыкания
ключа будет рассчитываться по формуле:
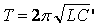
а период колебаний, после замыкания
ключа
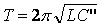
- где С' -
емкость батареи конденсаторов до
замыкания ключа, С'' -
емкость батареи после замыкания ключа.
Используя полученные выражения, запишем уравнение для
искомой величины:
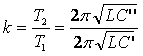
после сокращения, получим равенство:
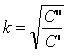 . .
Получим выражения для емкостей батарей конденсаторов до и
после замыкания ключа.
До замыкания ключа батарея представляет собой два
параллельных участка состоящих из двух последовательных конденсаторов
емкостями С1 и С2. Емкость каждого
последовательного участка будет рассчитываться по формуле:
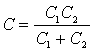
тогда емкость батареи при разомкнутом ключе:
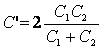 . .
После замыкания ключа батарея будет представлять собой два
последовательных участка, каждый из которых состоит из двух параллельных
конденсаторов емкостями С1 и С2. Емкость двух
конденсаторов, соединенных параллельно:
С=С1+С2.
Тогда емкость батареи после замыкания ключа:
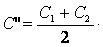
Подставим полученные выражения в уравнение для искомой
величины k:
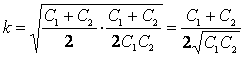 . .
Подставим численные значения и рассчитаем результат:
 |
|
Ответ: Период колебаний
возрастет в 1,25 раза.
------------------------------------------------------------------ |
|
|
|
|
|
|
|
|
|
|
|
_____________________________________________________________________ |
|
|
|
Содержание |
| |
|
|
|
|
|
