| |
|
|
|
|
| Банк заданий ЕГЭ
по теме "Кинематика" |
|
|
|
|
|
|
|
| |
|
Контрольная работа
по теме "Кинематика" |
|
|
| |
| |
|
Задачи для самостоятельного решения
по теме "Кинематика" |
| |
Кинематика равномерного движения.
Относительность движения. |
|
№
1.1.



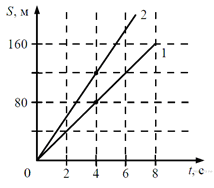
На рисунке
представлены графики зависимости пройденного
пути от времени для двух тел. На сколько
скорость второго тела υ2
больше скорости первого тела υ1?
Решение:
Ответ:
Скорость второго тела больше скорости первого
на величину 10 м/с |
 |
|
|
111 |
|
|
|
№
1.2.



Координата материальной точки
изменяется с течением времени по закону
x=3
– 2t.
Какой из приведённых ниже графиков соответствует этой
зависимости?
Решение:
Ответ:
4 |
|
|
|
111 |
|
|
|
№
1.3.



Тело, двигаясь прямолинейно и равномерно в
плоскости, перемещается из точки А с координатами (0;2)
в точку В с координатами (4;-1), за время равное 10 с.
Найдите модуль скорости тела?
Решение:
Ответ:
0,5
м/с |
|
|
|
111 |
|
|
|
№
1.4.



Туристы прошли сначала 400 м на
северо-запад, затем 500 м на восток и еще 300 м на
север. Найти геометрическим построением модуль и
направление их перемещения.
Решение:
Ответ:
620 м, 20˚ к направлению на север. |
|
|
|
111 |
|
|
|
№
1.5.



По прямолинейной автостраде движутся
равномерно: автобус - вправо со скоростью 20 м/с,
легковой автомобиль - влево со скоростью 15 м/с,
мотоциклист - влево со скоростью 10 м/с. Координаты этих
экипажей в момент начала наблюдений равны
соответственно: 500, 200 и -300 м. Написать их уравнения
движения. Найти:
а) координату автобуса через 5 с;
б) координату легкового автомобиля и
пройденный путь через 10 с;
в) через какое время координата
мотоциклиста будет равна -600 м;
г) в какой момент времени автобус
проезжал начало координат;
д) где был легковой автомобиль за 20 с
до начала наблюдения.
Решение:
Ответ:
|
|
|
|
111 |
|
|
|
№
1.6.



Движения двух велосипедистов заданы
уравнениями: x1=5t
и
x2=150 - 10t. Найти место и время
встречи велосипедистов. Задачу решить графически и
аналитически.
Решение:
Ответ:
50 м, 10с. |
|
|
|
111 |
|
|
|
№
1.7.



Движение грузового автомобиля описывается уравнением х1= - 270 +12t,
а движение пешехода по обочине того же шоссе –
уравнением х2= - 1,5t.
Сделать пояснительный рисунок, на котором указать
положение автомобиля и пешехода в момент начала
наблюдения. С какими скоростями и в каком направлении
они двигались? Когда и где они встретились?
Решение:
Ответ:
Скорость автомобиля 12 м/с, направлена
вдоль оси Х, скорость пешехода 1,5 м/с, направлена в
сторону – противоположную оси Х, автомобиль и пешеход
встретятся через 20 с, в точке с координатой( – 30) м. |
|
|
|
111 |
|
|
|
№
1.8.



Поезд длиной 200 м въезжает на мост со
скоростью 5 м/с. За сколько времени поезд пройдет весь
мост, если длина моста 300 м?
Решение:
Ответ:
100 с. |
|
|
|
111 |
|
|
|
№
1.9.



Мяч, брошенный с земли вертикально вверх
достиг высоты 10 м и затем был пойман на балконе на
высоте 6 м от земли. Найдите путь и модуль перемещения
мяча.
Решение:
Ответ:
L = 14
м,
S = 6
м. |
|
|
|
111 |
|
|
|
№
1.10.



Мяч упал с высоты 2 м, отскочил на 1 м
вверх, снова упал и после отскока был пойман на высоте
0,5 м от пола. Найдите пройденный мячом путь и модуль
перемещения.
Решение:
Ответ:
L = 4,5
м,
S =
1,5
м. |
|
|
|
111 |
|
|
|
№
1.11.



Поезд движется со скоростью 50 км/ч, а
пассажир идет по вагону со скоростью 4 км/ч. Какова
скорость движения этого пассажира относительно земли,
если он идет в сторону головного вагона?
Решение:
Ответ:
54 км/ч. |
|
|
|
111 |
|
|
|
№
1.12.



Поезд движется со скоростью 54 км/ч, а
проводник идет по вагону со скоростью 3 км/ч. Какова
скорость движения проводника относительно земли, если он
идет в сторону последнего вагона?
Решение:
Ответ:
51 км/ч |
|
|
|
111 |
|
|
|
№
1.13.



Два автомобиля движутся по одному и тому
же шоссе в противоположных направлениях, один со
скоростью 36 км/ч, другой со скоростью 72 км/ч. Какова
скорость второго автомобиля в системе отсчета связанной
с первым автомобилем? Ответ дать в СИ.
Решение:
Ответ:
30 м/с. |
|
|
|
111 |
|
|
|
№
1.14.



Два автомобиля движутся по одному и тому
же шоссе в одном направлении, один со скоростью 20 м/с,
а второй его догоняет со скоростью 90 км/ч. Какова
скорость второго автомобиля в системе отсчета связанной
с первым автомобилем? Ответ дать в СИ.
Решение:
Ответ:
5 м/с. |
|
|
|
111 |
|
|
|
№
1.15.



Найти скорость лодки относительно берега
реки, если скорость лодки относительно воды равна 8 м/с
и направлена перпендикулярно берегу реки, а скорость
течения 6 м/с.
Решение:
Ответ:
10 м/с. |
|
|
|
111 |
|
|
|
№
1.16.



Небольшое тело движется в пространстве. На рисунке
показаны графики зависимости от времени t проекций Vx, Vy иVz скорости этого
тела на оси OX, OY и OZ.
Чему равен модуль скорости этого тела в момент времени t = 4
с? (Ответ дайте в метрах в секунду.)
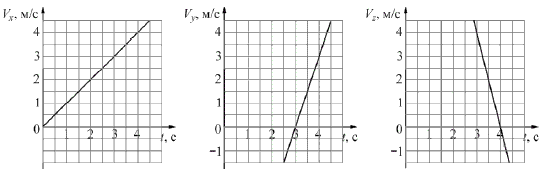
Решение:
При движении тела в пространстве его скорость в любой момент
времени можно представить как геометрическую сумму составляющих его скорости
относительно каждой из осей:
где
Vx, Vy
и
Vz
- скорости тела
относительно каждой из осей координат соответственно.
Поскольку оси взаимно
перпендикулярны, то численное значение скорости можно рассчитать как:
Ответ:
5 м/с |
|
|
|
111 |
|
|
|
№
1.17.



Скорость движения лодки относительно воды в
3 раза больше скорости течения реки. Во сколько раз
больше времени займет поездка на лодке между двумя
пунктами против течения, чем по течению? Движение лодки,
как по течению, так и против течения считать
равномерным.
Решение:
Ответ:
В 2 раза. |
|
|
|
111 |
|
|
|
№
1.18.



Два поезда движутся навстречу друг другу со скоростями
72 и 54 км/ч. Пассажир, находящийся в первом поезде,
замечает, что второй поезд проходит мимо него за 14
секунд. Какова длина второго поезда?
Решение:
Ответ:
Длина второго поезда составляет 490 м. |
|
|
|
111 |
|
|
|
|
|
111 |
|
|
|
|
|
111 |
|
|
|
Кинематика неравномерного движения. Равноускоренное
движение. |
|
|
|
№
1.21.



Первую половину пути автомобиль двигался с постоянной
скоростью 40 км/ч, а вторую половину пути с постоянной
скоростью 80 км/ч. Чему равна средняя скорость
автомобиля?
Решение:
Ответ:
Средняя скорость автомобиля составила
53,3 км/ч. |
|
|
|
111 |
|
|
|
№
1.22.



Первую половину времени автомобиль двигался с постоянной
скоростью 40 км/ч, а вторую половину времени с
постоянной скоростью 80 км/ч. Чему равна средняя
скорость автомобиля.
Решение:
Ответ:
60 км/ч. |
|
|
|
111 |
|
|
|
№
1.23.



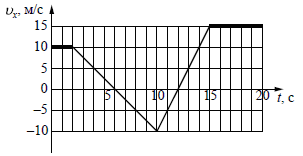
На
рисунке приведён график зависимости проекции скорости
тела υх от времени.
Чему равна проекция
ускорения этого тела ax
в интервале времени от 6 с до 10 с?
Решение:
Ответ:
- 2,5 м/с2. |
 |
|
|
111 |
|
|
|
№
1.24.



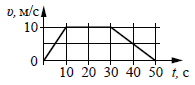
На
рисунке представлен график зависимости модуля скорости
υ автомобиля от времени t. Определите по
графику путь, пройденный автомобилем в интервале времени
от 0 до 30 с.
Решение:
Ответ:
Путь, пройденный автомобилем за 30
секунд равен 250 метров. |
 |
|
|
111 |
|
|
|
№
1.25.



На
рисунке представлен график зависимости модуля скорости
υ автомобиля от времени t. Определите по
графику путь, пройденный автомобилем в интервале времени
от 0 до 5 с.
Решение:
Ответ:
35 метров. |
 |
|
|
111 |
|
|
|
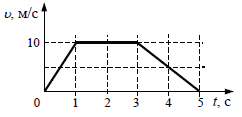
№
1.26.



На рисунке представлен график зависимости модуля
скорости υ автомобиля от времени t.
Определите по графику путь, пройденный автомобилем в
интервале времени от 0 до 3 с.
Решение:
Ответ:
25 метров. |
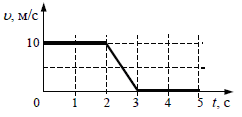 |
|
|
111 |
|
|
|
№
1.27.



Поезд через 10 с после начала движения
приобретает скорость 0,6 м/с. Через какое время от
начала движения скорость поезда станет равной 3 м/с?
Решение:
Ответ:
50 с. |
|
|
|
111 |
|
|
|
№
1.28.



Велосипедист движется под уклон с
ускорением 0,3 м/с2. Какую скорость
приобретет велосипедист через 20 с, если его начальная
скорость равна 4 м/с?
Решение:
Ответ:
10 м/с. |
|
|
|
111 |
|
|
|
№
1.29.



За какое время автомобиль, двигаясь с
ускорением 0,4 м/с2, увеличит свою скорость с
12 до 20 м/с?
Решение:
Ответ:
20 с. |
|
|
|
111 |
|
|
|
№
1.30.



Автомобиль начинает движение из состояния
покоя и проходит первую половину пути с ускорением а1,
при этом его скорость увеличивается до 10 м/с. Вторую
половину пути автомобиль проходит с ускорением а2,
при этом его скорость увеличивается еще на 5 м/с. Что
больше а1
или а2
, и во сколько раз?
Решение:
Ответ:
На второй половине пути ускорение
автомобиля больше в 1,25 раза. |
|
|
|
111 |
|
|
|
№
1.31.



Зависимость скорости от времени при
разгоне автомобиля задана формулой υx
= 0,8t. Построить график
зависимости скорости от времени и найти скорость в конце
пятой секунды.
Решение:
Ответ:
4 м/с. |
|
|
|
111 |
|
|
|
№
1.32.



Во сколько раз скорость пули при вылете
из ствола отличается от скорости пули в середине ствола?
Решение:
Ответ:
Скорость пули при вылете из ствола в
раза больше, чем в середине
ствола. |
|
|
|
111 |
|
|
|
№
1.33.



Уклон длиной 100 м лыжник прошел за 20 с,
двигаясь с ускорением 0,3 м/с2. какова
скорость лыжника в начале и в конце уклона?
Решение:
Ответ:
2 м/с и 8 м/с. |
|
|
|
111 |
|
|
|
№
1.34.



Стрелу выпустили вертикально вверх с
начальной скоростью 35 м/с. Куда будет направлена, и
чему будет равна по модулю скорость стрелы через 3
секунды после выстрела? Сопротивлением воздуха
пренебречь.
Решение:
Ответ:
Направлена вверх и равна 5 м/с. |
|
|
|
111 |
|
|
|
№
1.35.



Автомобиль, двигаясь со скоростью 18 км/ч,
ускорился до 72 км/ч за 10 секунд. Какой путь проехал
автомобиль за это время?
Решение:
Ответ:
125 м. |
|
|
|
111 |
|
|
|
№
1.36.



Автомобиль начал движение с ускорением 0,5
м/с2
в тот момент, когда мимо него равномерно проезжал
трамвай со скоростью 5 м/с. Через сколько времени
автомобиль догонит трамвай?
Решение:
Ответ:
20 с. |
|
|
|
111 |
|
|
|
№
1.37.



Скорость палубного истребителя на взлете
360 км/ч. С каким минимальным постоянным ускорением он
должен двигаться при разгоне, если длина взлетной полосы
300 м, а катапульта придает ему начальную скорость 50
м/с.
Решение:
Ответ:
12,5 м/с2. |
|
|
|
111 |
|
|
|
№
1.38.



Тело свободно падает с высоты 80 м. Каково
его перемещение за последнюю секунду падения?
Решение:
Ответ:
35 м. |
|
|
|
111 |
|
|
|
№
1.39.



Пловец, спрыгнув с пятиметровой вышки,
погрузился в воду на глубину 2 м. Сколько времени и с
каким по модулю ускорением он двигался в воде?
Решение:
Ответ:
0,4 с, 25 м/с2. |
|
|
|
111 |
|
|
|
№
1.40.



Камень,
брошенный с поверхности земли почти вертикально вверх,
через 3 с. после броска упал на крышу дома со скоростью
10 м/с. На какой высоте от поверхности земли находится
крыша? Сопротивление воздуха пренебрежимо мало.
Решение:
Ответ:
15 м. |
|
|
|
111 |
|
|
|
№
1.41.



Камень,
брошенный с поверхности земли вертикально вверх, на
высоте 25 метров побывал дважды, с интервалом в 4
секунды. С какой скорость был брошен камень?
Сопротивление воздуха пренебрежимо мало.
Решение:
Ответ:
30 м/с. |
|
|
|
111 |
|
|
|
№
1.43.



Автомобиль трогается с места с
ускорением 2 м/с2.
Какой путь он пройдет за 3-ю и 4-ю секунды движения?
Решение:
Ответ:
5 м, 7 м. |
|
|
|
111 |
|
|
|
№
1.44.



За 2,5 с.
прямолинейного равноускоренного движения тело прошло
путь 40 м, увеличив свою скорость в 3 раза. Какова
начальная скорость тела?
Решение:
Ответ:
8 м/с. |
|
|
|
111 |
|
|
|
№
1.45.



Ускорение
лыжника на одном из спусков трассы равно 2,4 м/с2.
На этом спуске его скорость увеличивается на 36 м/с.
Чему равно время спуска лыжника по трассе?
Решение:
Ответ:
15 с. |
|
|
|
111 |
|
|
|
№
1.46.



С аэростата, зависшего над Землей упал
груз. Через 10 с он достиг поверхности Земли. На какой
высоте находился аэростат? Сопротивление воздуха
пренебрежимо мало.
Решение:
Ответ:
500 м. |
|
|
|
111 |
|
|
|
|
|
111 |
|
|
|
|
|
111 |
|
|
|
|
|
111 |
|
|
|
|
|
111 |
|
|
|
Кинематика движения по окружности.
|
|
|
|
№
1.51.



Шарик движется по окружности
радиусом r со скоростью υ. Как изменится
центростремительное ускорение шарика, если его скорость
увеличить в 3 раза?
Решение:
Ответ:
Центростремительное ускорение
увеличится в 9 раз. |
|
|
|
111 |
|
|
|
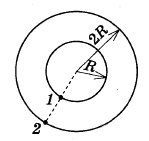
№
1.52.



Два
велосипедиста совершают кольцевую гонку с
одинаковой угловой скоростью. Положения и
траектории движения велосипедистов показаны на
рисунке. Чему равно отношение линейной скорости
первого велосипедиста к линейной скорости
второго?
Решение:
Ответ:
0,5. |
 |
|
|
111 |
|
|
|
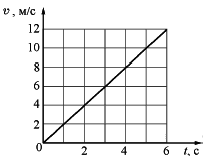
№
1.53.



Материальная точка движется по окружности
радиусом 4 м. На графике показана зависимость
модуля её скорости от времени. Чему
равен модуль центростремительного ускорения
точки в момент t = 3 с?
Решение:
Ответ:
9 м/с2. |
 |
|
|
111 |
|
|
|
№
1.54.



Каково центростремительное ускорение
поезда, движущегося по закруглению дороги радиусом 800 м
со скоростью 20 м/с?
Решение:
Ответ:
0,5 м/с2. |
|
|
|
111 |
|
|
|
№
1.55.



Ведущее колесо электровоза диаметром 1 м
делает 10 оборотов за 2 секунды. С какой скоростью
движется электровоз?
Решение:
Ответ:
15,7 м/с. |
|
|
|
111 |
|
|
|
№
1.56.



Волчок, вращаясь равномерно с частотой 25
оборотов в секунду, свободно падает с высоты 20 м.
Сколько оборотов сделает волчок за время падения?
Решение:
Ответ:
50. |
|
|
|
111 |
|
|
|
№
1.57.



Определить с какой скоростью поднимается
груз, если барабан лебедки на который наматывается трос,
вращается с угловой скоростью 6 рад/с и имеет диаметр
0,2 м.
Решение:
Ответ:
0,6 м/с. |
|
|
|
111 |
|
|
|
№
1.58.



Линейная скорость точек на краю
вращающегося диска 3 м/с. Точки расположенные на 10 см
ближе к оси вращения имеют линейную скорость 2 м/с. Чему
равен радиус диска?
Решение:
Ответ:
0,3 м |
|
|
|
111 |
|
|
|
№
1.59.



Вычислить скорость Луны относительно
Земли. Луна совершает полный оборот вокруг Земли за 28
суток, расстояние от Луны до Земли 3,84∙108
м.
Решение:
Ответ:
997 м/с. |
|
|
|
111 |
|
|
|
№
1.60.



Тело, движущееся по окружности радиусом 9
м с постоянной скоростью, имеет центростремительное
ускорение 4 м/с2.
Определить период движения с точностью до сотых?
Решение:
Ответ:
9,42 с. |
|
|
|
111 |
|
|
|
№
1.61.



Радиус рукоятки колодезного ворота в 3
раза больше радиуса вала, на который наматывается трос.
Какова линейная скорость конца рукоятки при равномерном
поднятии ведра с глубины 10 м за 20 с?
Решение:
Ответ:
1,5 м/с. |
|
|
|
111 |
|
|
|
№
1.62.



Диск радиусом 20 см равномерно вращается
вокруг своей оси. Скорость точки, находящейся на
расстоянии 15 см от центра диска равна 1,5 м/с. Какова
скорость крайних точек диска?
Решение:
Ответ:
2 м/с. |
|
|
|
111 |
|
|
|
№
1.63.



Две материальные точки движутся по
окружностям радиусами R1
и R2=2R1
c одинаковыми по модулю
скоростями. Как относятся периоды обращения этих
материальных точек?
Решение:
Ответ:
Т2=2Т1. |
|
|
|
111 |
|
|
|
№
1.64.



Найти линейную скорость точек земной поверхности
расположенных на 55 параллели (г.Вязьма), в следствии
суточного вращения Земли вокруг своей оси.
Решение:
Ответ:
Линейная скорость точек земной поверхности в районе
Вязьмы составляет примерно 267 м/с. |
|
|
|
111 |
|
|
|
№
1.65.



Спутник движется по круговой орбите на
высоте 400 км вокруг планеты радиусом 5000 км. Каковы
скорость и ускорение спутника, если период его обращения
81 мин?
Решение:
Ответ:
7 км/с, 9 м/с2. |
|
|
|
111 |
|
|
|
|
|
111 |
|
|
|
|
|
111 |
|
|
|
|
|
111 |
|
|
|
|
|
111 |
|
|
|
|
|
111 |
|
|
|
|
|
Кинематика движения тела под углом к горизонту. |
|
|
|
№
1.71.



Тело брошено с поверхности земли с
начальной скоростью 20 м/с. Под каким углом к
поверхности земли было брошено тело, если он находилось
в полете 2 с?
Решение:
Ответ:
30˚. |
|
|
|
111 |
|
|
|
№
1.72.



Тело брошено с поверхности земли под углом
30˚ к горизонту. Во сколько раз максимальная скорость
полета больше минимальной?
Решение:
Ответ:
раз. |
|
|
|
111 |
|
|
|
№
1.73.



Снаряд, вылетевший из орудия под углом к
горизонту, находился в полете 12 с. Какой наибольшей
высоты достиг снаряд?
Решение:
Ответ:
180 м. |
|
|
|
111 |
|
|
|
№
1.74.



Футбольный мяч пролетел после удара
расстояние 60 м. Какую начальную скорость сообщили мячу,
если высота верхней точки его траектории 20 м?
Решение:
Ответ:
25 м/с. |
|
|
|
111 |
|
|
|
№
1.75.



Вратарь, выбивая мяч от ворот (с земли)
сообщил ему скорость 20 м/с, направленную под углом 50˚
к горизонту. Найти время полета мяча, максимальную
высоту подъема и дальность полета.
Решение:
Ответ:
3,1 с; 12 м; 40 м. |
|
|
|
111 |
|
|
|
№
1.76.



Небольшой камень бросили с ровной
горизонтальной поверхности земли под углом к горизонту.
На какую максимальную высоту поднялся камень, если ровно
через 1 секунду после броска его скорость была
направлена горизонтально?
Решение:
Ответ:
5 м. |
|
|
|
111 |
|
|
|
№
1.77.



Мяч брошен горизонтально со скоростью 12
м/с из окна дома, находящегося на высоте 20 м от
поверхности земли. На каком расстоянии от дома он упадет
на землю?
Решение:
Ответ:
24 м. |
|
|
|
111 |
|
|
|
№
1.78.



Мяч бросили горизонтально с высоты
h и он упал на землю через 3
с. С какой высоты был брошен мяч?
Решение:
Ответ:
45 м. |
|
|
|
111 |
|
|
|
№
1.79.



С некоторой
высоты Н свободно падает стальной шарик. Через
t
= 1 с после начала падения он сталкивается с неподвижной
плитой, плоскость которой наклонена под углом 45° к
горизонту, и до момента падения на Землю пролетает по
горизонтали расстояние
S
= 20 м. Каково значение Н? Сопротивление воздуха не
учитывать. Удар шарика о плиту считать абсолютно
упругим.
Решение:
Ответ:
Шарик упал с высоты 25 м. |
|
|
|
111 |
|
|
|
|
|
111 |
|
|
|
|
|
|
